题解:P10377 [GESP202403 六级] 好斗的牛

题解:P10377 [GESP202403 六级] 好斗的牛
xyx404
思路:
考虑到 的最大值只有九,所以可以使用 dfs 算法枚举组合方案,把每一头牛的放置顺序存入一个数组中,当把所有的牛都放好后,算出需要的牛棚,最后输出最小值就可以了。
如何算出需要的牛棚,先画张图。
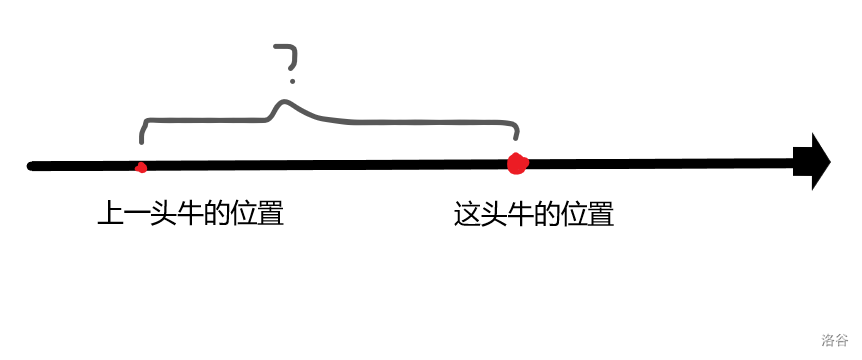
观察这张图,可以分四种情况。
第一种情况,上一头牛的 大于现在这头牛的 ,那么距离是上一头牛的 ,如下图。
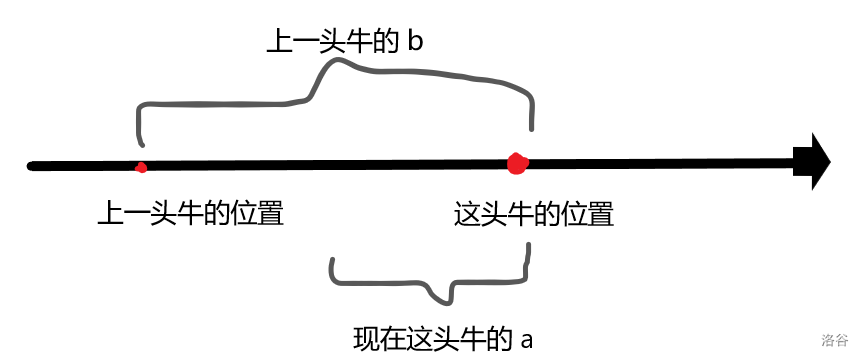
第二种情况,上一头牛的 等于现在这头牛的 ,那么这两个数都可以是距离,如下图。
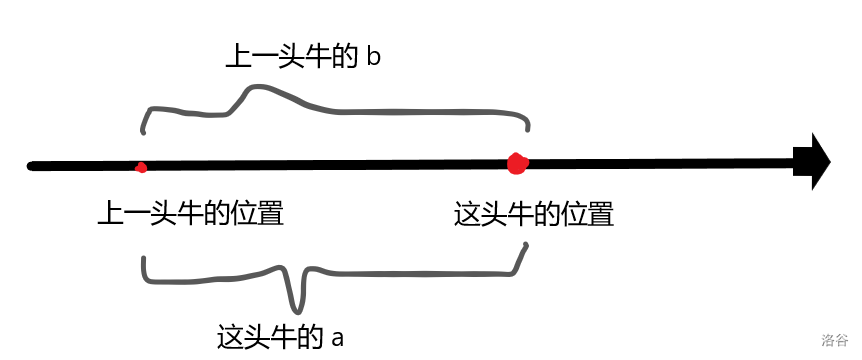
第三种情况,上一头牛的 小于现在这头牛的 ,那么距离是这头牛的 ,如下图。
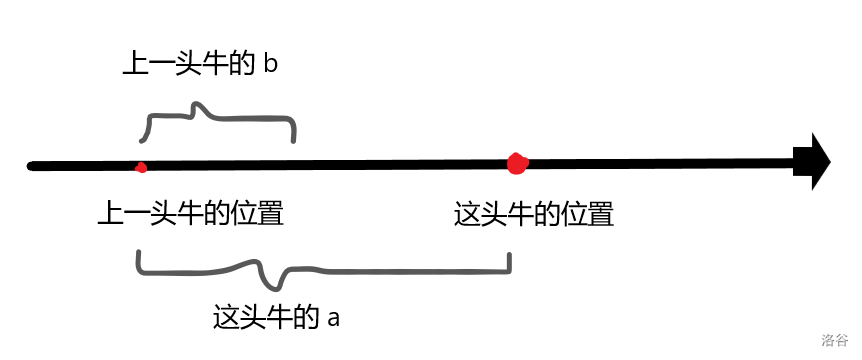
第四种情况,没有上一头牛,也就是第一头牛,没有距离,循环直接从第二个放入牛的开始,如下图。
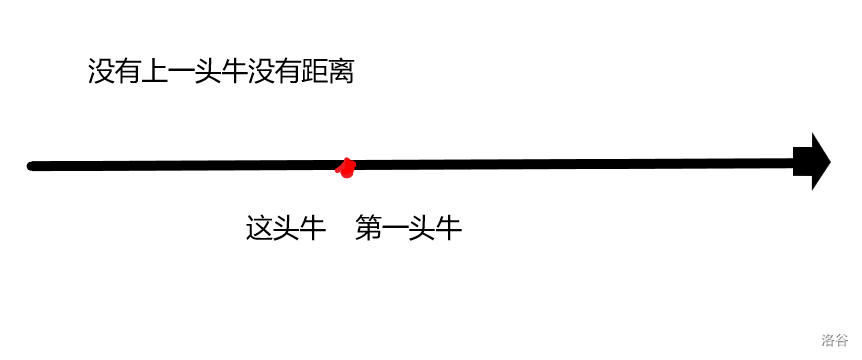
通过上述分析可以看出,距离是上一头牛的 与这头牛的 中的最大值。
需要注意的是求完距离后要考虑这一头牛也需要一个牛棚,所以每次求出距离后还要加一才可以算出需要的牛棚,要提前处理第一头牛,可以直接将求需要的牛棚的变量赋值为一。
完整代码带注释:
代码与思路完全相同。
|
评论
匿名评论隐私政策
✅ 你无需删除空行,直接评论以获取最佳展示效果











